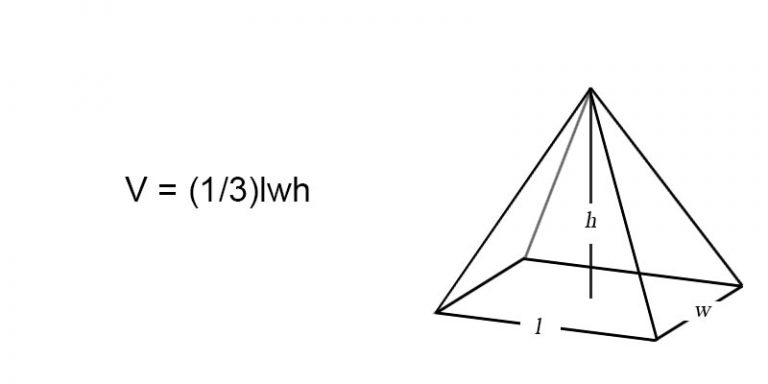
Volume of Pyramid 

We can define volume as the space which is occupied by the sides of a shape. Like every other geometrical shape, a pyramid also has its own formula for volume. A pyramid can be defined as a three-dimensional figure whose faces are triangularly connected to each other. The mathematical formula given to find the volume of pyramid is: ⅓ * b * h where ‘b’ is the base and ‘h’ is the height of the pyramid. There are various types of pyramids such as square pyramid, right pyramid, rectangular pyramid, and many others. In this article, we will try to learn some basic aspects of the pyramid such as properties of the pyramid and examples related to the volume of the pyramid. 

Some Significant Properties of Pyramid 

A pyramid can be defined as a three-dimensional figure whose faces are triangularly connected to each other. As with every other geometrical shape, a pyramid also possesses some properties which are significant in aspects of solving calculations. The following points analyze the important properties of a pyramid.

• If you observe the shape of the pyramid, it is made up of three vital parts: the apex, the base, and the face. The apex of a pyramid can be defined as the highest point whereas the base is the lowest point of a pyramid. 
• We know that a pyramid is categorized under various types. One of those types is a regular polygon, if the pyramid is a regular polygon then the sides are considered as a congruent one. 
• The base of the polygon is considered to be square. It is a shape that is made up of four equal and parallel sides. 

Examples Related to the Volume of Pyramid 

As mentioned above, the mathematical formula given to calculate the volume of a pyramid is ⅓ * b * h where ‘b’ is the base and ‘h’ is the height of the pyramid. Let us try to solve some examples related to finding the volume. 

Example 1: Find out the volume of the pyramid if the base and height of the pyramid are 12 cm and 8 cm respectively? 

Solution: Given that, 

The base of the pyramid = 12 cm 

Height of the pyramid = 8 cm 

Using the formula of volume of pyramid = ⅓ * b * h

⅓ * 12 * 8 = 4 * 8 

4 * 8 = 32 cm cubic units. 

Therefore, the volume of the pyramid is = 32 cm cubic units. 

Example 2: Calculate the volume of the pyramid if the base and height of the pyramid is 18 cm and 9 cm respectively? 

Solution: Given that, 

Base of the pyramid = 18 cm 

Height of the pyramid = 9 cm 

Using the formula of pyramid volume = ⅓ * b * h

⅓ * 18 * 9 = 18 * 3 

18 * 3 = 54 cm cubic units. 

Hence, the volume of the pyramid is = 54 cm cubic units. 

Example 3:

Find out the volume of the pyramid if the base and height of the pyramid are 15 cm and 9 cm respectively? 

Solution: Given that, 

Base of the pyramid = 15 cm 

Height of the pyramid = 9 cm 

Using the formula of volume of pyramid = ⅓ * b * h

⅓ * 15 * 9 = 15 * 3 

15 * 3 = 45 cm cubic units. 

Thus, the volume of the pyramid is = 45 cm cubic units. 

Visit Cuemath’s website if you want to study these topics in an interesting, detailed, and fun way. 

Master Math from Cuemath Math Classes 

Cuemath is considered to be one of the leading platforms and websites for teaching mathematics. It covers various aspects such as brain training with the help of math games puzzles for arithmetic progression. Cuemath also provides you with math classes where you will find highly qualified and experienced teachers. Therefore, if you want to study math in a different manner, visit Cuemath and grab every opportunity. Book a free session now.